[물리전자공학] 2. 전자와 정공 (Electron & Hole)

 

지난글에서는 반도체의 소재인 실리콘의 결정 구조와 이와 관련된 다양한 용어에 대해 알아보았다.

1. 반도체 기초 - 실리콘의 결정 구조

 

이번 글에서는 전자와 정공(Hole)에 대해 공부해보려 한다. 

정말 정말 정말 중요한 개념이다.

반도체 공부의 시작의 시작의 시작의 시작을 담당하는 개념이다.

 

실리콘의 결정구조 (출처: https://www.eeweb.com/how-semiconductors-work/)

 

지난 글에서 보았던 실리콘의 결정구조 그림을 다시 가져와 보겠다.

불순물이나 결함이 없는, 완벽히 실리콘으로만 이루어졌다고 가정하자.

 

절대 영도(0K)의 환경에서 실리콘 결정 속 전자들은 모두 실리콘 원자핵에 속박된 상태다.

즉, 전자들이 움직일 수 없다는 것이다.

그러니까... 전류가 흐를 수가 없다.

 

하지만! 우리가 살고 있는 이 세계는 절대 영도가 아니지 않은가?!

상온에서는 이 실리콘 원자 간의 공유 결합이 완전히 유지되지 못하고 조금은 깨져버린다.

이렇게 공유 결합에서 탈출한 전자들은 언제든 움직일 수 있는 상태가 된다.

 

전자와 정공 (출처: https://energyeducation.ca/encyclopedia/Electron_hole)

 

 

그렇게 전자가 원래 있던 자리는 비게 되는데, 이 자리를 Hole(정공) 이라고 한다.

별 거 아니다. 그냥 전자의 빈 자리다.

위 그림을 참고하면 이해가 쉽다.

 

 

그런데 이 Hole이라는게, 반도체에서의 현상을 설명할 때 꽤나 많이 쓰인다.

전자가 원래 자리에 잘 있는 상태는 전기적으로 중성을 띤다.

전자는 전기적 음극을 띤다.

그럼.. 전자가 있던 공간은 전기적 양극을 띤다고 할 수 있는 거 아닌가?! (오)

 

이런 식으로 전자가 있던, 비어버린 공간을 전기적 양성을 띤 어떠한 가상의 입자로 받아들임으로써

전자의 움직임이 띠는 양상의 반대로 이해할 수 있게 된거다.

반도체에서 일어나는 여러 현상들을 전자 이동 현상으로만 설명하지 않고,

Hole의 이동으로도 설명할 수 있게 되었다는 이야기다.

 

 

예를 들어보자.

외부에서 전압을 걸어주면, 전자는 (+) 방향으로 이동한다.

그럼 반대로, Hole은 (-) 방향으로 이동한다.

이렇게 같은 현상을 전자와 Hole의 관점에서 두 가지 방식으로 표현할 수 있다!

 

그렇다면 당연하게도, 열 평형 상태에서 자유전자의 농도와 Hole의 농도는 같을 것이다.

이 때 자유전자의 농도는 n (negative), hole의 농도는 p (positive) 라는 기호로 표현한다.

열 평형 상태에서 n = p 로 표현할 수 있다.

 

 

또 여기서 중요한 개념이 나온다.

바로 Intrinsic carrier concentration (진성 캐리어 농도) 이다.

Carrier, 무엇인가를 "옮겨주는 것"을 뜻한다.

반도체에서의 carrier는 전하를 옮겨주는 매개, 즉, 전자와 정공(Hole)인 것이다. 

이 진성 캐리어 농도는 단위 부피 당 공유 결합을 탈출한 전자의 개수를 의미한다.

단위 부피 당 개수이기 때문에 단위는 [cm^-3] 를 사용한다.

온도와 물질 별 진성 캐리어 농도 (출처: https://www.tf.uni-kiel.de/matwis/amat/semi_en/kap_2/illustr/i2_2_3.html)

 

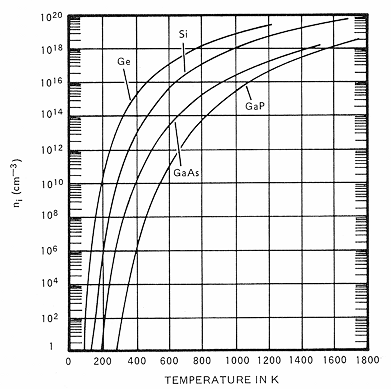
당연하게도, 온도가 높을 수록 더 많은 전자가 공유 결합에서 탈출한다.

온도가 높을 수록 진성 캐리어 농도가 높아진다는 소리다.

온도와 물질에 따라 이 진성 캐리어 농도의 값도 달라지는데, 모두 상수값이다.

위 그래프를 참고하면, 상온(300K)에서 실리콘의 진성 캐리어 농도 값은, 약 1.5 10^10 [cm^-3] 이다.

 

실리콘의 단위 부피 당 원자 개수가 5*10^22 [cm^-3] 임을 생각하면,

실리콘은 상대적으로 높은 전기저항도를 가지고 있다고도 여길 수 있겠다.

 

 

 

오늘은 이렇게 간단하게 실리콘의 전자와 정공, 그리고 캐리어에 대한 개념을 알아보았다.

이제 드디어 다음 글에서는 에너지 밴드를 언급할 수 있다!

(사실 오늘 하려고 했는데 조금 피곤해서 내일 해야겠다 ㅜㅜ)

 

그럼, 다음 글에서 To be continued...