원래 1일 1 포스팅이 원칙이었으나.. 최근 좀 바빴다.
이제야 올리는 에너지 밴드갭에 대한 내용
지난 포스팅에서 에너지 밴드가 무엇이며, 그것이 왜 생기는지에 대해 정성적으로 다루어보았다.
1.4 반도체 기초 - 에너지 밴드 (Energy band) (1)
그렇게 다루고 싶었던 에너지 밴드에 대해 드디어 포스팅을 할 수 있게 되었다! :)이 포스팅을 읽기 전에, 이전 포스팅을 통해 단일 실리콘 원자에서의 에너지 레벨에 대해 복습하자. 1.3 반도체
hyenny0909.tistory.com
오늘은 조금 정량적으로 풀어볼까 한다.
분명 지난 포스팅 마지막에 "정성적인 내용으로 이어가겠다!" 했는데..ㅎ..
에너지 밴드 이론을 다루기 위해서는 이걸 한 번은 언급해야 하기 때문에 어쩔 수 없다ㅠㅠ
이해하기 어려운 분들은 이 포스팅을 패스하셔도 괜찮습니다...죄송합니다
어려운 거 맞아요...
에너지 밴드를 구하려면, 파동함수를 구하면 된다.
파동함수를 구하려면? 슈뢰딩거 방정식을 풀면 된다.
슈뢰딩거 방정식을 풀려면? 퍼텐셜 함수를 알아야 한다!
목표: 고체 함수의 파동함수로 에너지 밴드 유추하기
첨부터 냅다 고체로 시작하는 건 너무하니까 단일 원자의 퍼텐셜 모양부터 보자.

단일 원자의 퍼텐셜 함수는 위와 같이 생겼다.

근데 이제 여러 개의 원자들이 모여 고체를 이루면, 포텐셜이 겹치는 부분이 발생한다.

겹치는 부분을 남기면 이런 모양의 퍼텐셜이 된다.
이것이 바로 고체 구조에서의 퍼텐셜이다.
그치만.. 이런 곡선 모양의 퍼텐셜에 대해 슈뢰딩거 방정식을 풀어서...파동함수를 구하는 것은 너무 복잡해보이지 않나..
곡선이 어려우면? 직선으로 근사시키면 된다.

이렇게 말이다.
이렇게 근사시킨 모양을, 크로니 페니 모델 (Kronig-Penny Model)이라고 한다.
이렇게 생긴 퍼텐셜에 대해 슈뢰딩거 방정식을 풀어보겠다.

슈뢰딩거 방정식은 위와 같다.
맨 첫 줄이 오리지널이고.. 양변을 나누고 정리해서 우항을 0으로 만들어 보기 쉽게 만들었을 뿐
위의 크로니 페니 모델을 보면, 같은 퍼텐셜 모양이 공간에서 주기성을 띠며 반복되고 있다.
이 때 Bloch's Theorem을 쓰면 파동함수를 풀기가 더 쉬워진다.

슈뢰딩거 방정식은 파동함수에 대한 이차미분방정식을 풀어야 하기 때문에
미리 Bloch's theorem에 의해 주어지는 파동함수의 일반형에 대해 이차 미분을 해놓자.

그리고 아래 퍼텐셜 모양을 고려해서,

영역 I과 영역 II에 대한 슈뢰딩거 방정식을 쓰면 이렇게 된다.

여기에 아까 계산해놨던 Bloch's theorem에 의한 파동함수의 미분값과 이차미분값을 대입해보면,
아래와 같이 나온다.

이제 경계조건을 활용해 상수 A, B, C, D에 대한 관계식을 찾아내자.
그 경계 조건은 아래와 같다.
1) x=0 에서 파동함수의 값이 같아야 한다
2) x=0 에서 파동함수의 미분값이 같아야 한다
3) x=a에서의 와 x=-b에서의 파동함수 값이 같아야 한다
4) x=a 와 x=-b에서의 파동함수 미분값이 같아야 한다.
그러면 다음과 같은 식들을 얻을 수 있다.

직접 풀어 쓴거라 중간에 계산 실수가 있을 수도 있다
조금...미칠 것 같다...
여기까지만 내가 풀고..난 저 연립방정식들을 풀 자신이 없다.....
그러니 이미 똑똑한 분들이 다 풀어두신 걸 가져오겠다.

편-안
potential barrier 조건에 의해 V0은 무한대로, b는 0으로 근사시킬 수 있다.
아래는 근사시키는 과정이다.

이 근사식에 우리가 앞에서 가정한 베타와 알파에 대한 식을 대입하면 다음과 같은 식을 얻을 수 있다.

우변이 cos함수라는 것은, 좌변의 함수가 가질 수 있는 값이 -1과 1사이라는 것을 의미한다.
어찌저찌..
이에 대한 E-k diagram을 그리면 다음과 같다.

파란 네모 박스가 바로 고체 속 전자가 가질 수 있는 에너지의 크기를 의미한다.
파란 네모 박스 밖의 에너지 값은 전자가 절!대! 가질 수 없다. (지난 포스팅 참조)
k space를 줄여서 다시 그리면 다음과 같은 모양이 된다.
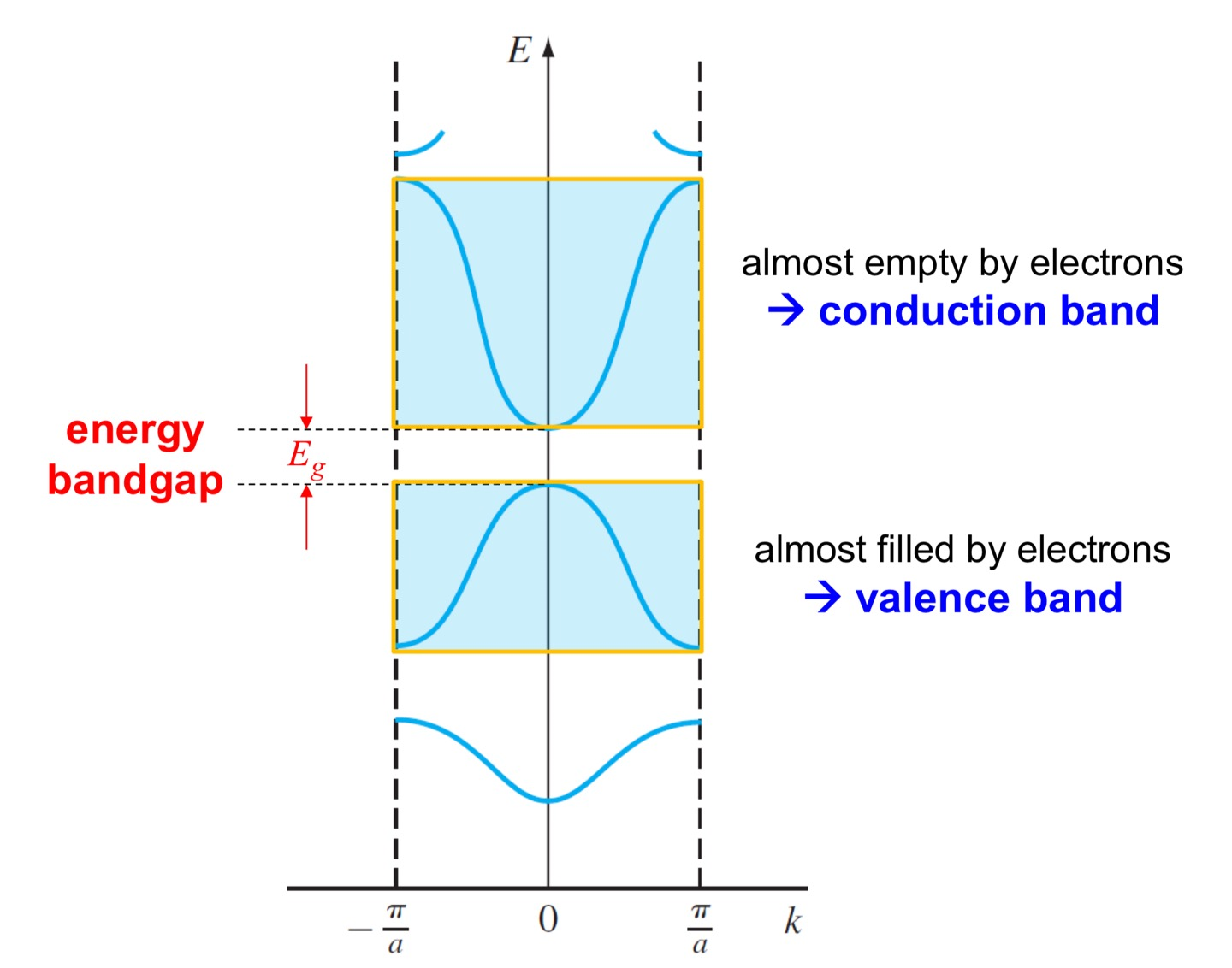
에너지 레벨은 양자화되어있지만, 그게 너무 촘촘한 나머지 지금과 같이 연속적으로 보이는 것이다.
그렇게 연속적으로 보이는 한 묶음을 에너지 밴드라고 부른다. (지난 포스팅에서 언급)
맨 아래에 있는 에너지 밴드는 최외각전자의 것이 아니므로 여기선 패스.
최외각전자의 에너지 밴드는 저 위에 두 개이다.
그 중 아래 것은 valence band로, 에너지가 더 낮기 때문에 대부분의 전자들이 여기에 몰려있다.
그 위의 conduction band에는 전자가 별로 없다.
그리고 conduction band의 가장 낮은 에너지 레벨인 Ec와
valence band의 가장 높은 에너지 레벨인 Ev의 차이,
그것을 에너지 밴드 갭 (Energy band gap)이라고 부른다.
원래 이번 포스팅에서 에너지 밴드 갭에 대해 더 자세히 다룰 예정이었는데,
에너지 밴드가 나오게 된 정량적인 경위를 다루려다보니 또 미뤄졌다.
그래도 포스팅하면서 공부 많이 된다.
다음 포스팅에서는 진짜!!! 에너지 밴드갭을 다룰것이다. 진짜.
'반도체 > 물리전자공학' 카테고리의 다른 글
| [물리전자공학] 7. 직접형 반도체와 간접형 반도체 (Direct bandgap & Indirect bandgap) (2) | 2024.10.03 |
|---|---|
| [물리전자공학] 6. 에너지 밴드 갭 (Energy band gap) (4) | 2024.10.02 |
| [물리전자공학] 4. 에너지 밴드 (Energy band) (2) | 2024.09.29 |
| [물리전자공학] 3. 단일 실리콘 원자에서의 에너지 준위 (4) | 2024.09.29 |
| [물리전자공학] 2. 전자와 정공 (Electron & Hole) (2) | 2024.09.28 |



